Laplace operator

http://en.wikipedia.org/wiki/Laplace_operator
Laplace operator được định nghĩa như sau:
The Laplace operator is a second order differential operator in the n-dimensional Euclidean space, defined as the divergence (∇·) of the gradient (∇ƒ). Thus if ƒ is a twice-differentiable real-valued function, then the Laplacian of ƒ is defined by

$\Delta f = \nabla^2 f = \nabla \cdot \nabla f,$ (1)

Ta đã biết gradient chính là vector có các thành phần là đạo hàm riêng phần của các biến thành phần:
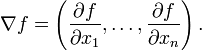
$\nabla f = \left(\frac{\partial f}{\partial x_1 }, \dots, \frac{\partial f}{\partial x_n } \right).$
Lại có công thức của devergence như sau:
The divergence of a vector field can be defined in any number of dimensions. If

$\mathbf{F}=(F_1, F_2, \dots, F_n),$

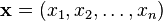in a Euclidean coordinate system where $\mathbf{x}=(x_1, x_2, \dots, x_n)$ and $d\mathbf{x}=(dx_1, dx_2, \dots, dx_n)$ , define

$\operatorname{div}\,\mathbf{F} = \nabla\cdot\mathbf{F} =\frac{\partial F_1}{\partial x_1} +\frac{\partial F_2}{\partial x_2}+\cdots +\frac{\partial F_n}{\partial x_n}.$

Suy ra: công thức của toán tử laplace:
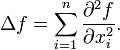$\Delta f = \sum_{i=1}^n \frac {\partial^2 f}{\partial x^2_i}.$ (2)
Chủ yếu chúng ta quan tâm đến công thức của toán tử laplace cho 2 chiều

Two dimensions

The Laplace operator in two dimensions is given by

$\Delta f = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$

where x and y are the standard Cartesian coordinates of the xy-plane.
In polar coordinates,

$\Delta f = {1 \over r} {\partial \over \partial r} \left( r {\partial f \over \partial r} \right) + {1 \over r^2} {\partial^2 f \over \partial \theta^2} .$

Nhật ký học tập và nghiên cứu - Hoàng Văn Hiệp

Thứ Năm, 30 tháng 9, 2010

Laplace operator

Two dimensions

Không có nhận xét nào:

Đăng nhận xét