In vector calculus, the gradient of a scalar field is a vector field which points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change.
Gradient là một vector
Ví dụ: Nhiệt độ trong một căn phòng là một đại lượng vô hướng T. Giả sử T không thay đổi theo thời gian, tại mỗi điểm trong căn phòng tọa độ (x, y, z) có một nhiệt độ nhất định, T(x, y, z)
Việc tính gradient của T tại một điểm, hướng của vector gradient sẽ chỉ cho ta biết hướng nào nhiệt độ tăng nhanh nhất tại điểm đó và độ lớn của vector gradient sẽ cho biết nhiệt độ tăng nhanh như thế nào
Definition:
The gradient (or gradient vector field) of a scalar function
 is denoted
is denoted  or
or  where
where  (the nabla symbol) denotes the vector differential operator, del. The notation
(the nabla symbol) denotes the vector differential operator, del. The notation  is also used for the gradient. The gradient of f is defined to be the vector field whose components are the partial derivatives of f. That is:
is also used for the gradient. The gradient of f is defined to be the vector field whose components are the partial derivatives of f. That is:The gradient of a vector
 is
is 
or the transpose of the Jacobian matrix
 .
.It is a second-rank tensor.
More generally, the gradient may be defined using the exterior derivative:

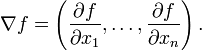

Không có nhận xét nào:
Đăng nhận xét