The convolution of ƒ and g is written ƒ∗g, using an asterisk or star. It is defined as the integral of the product of the two functions after one is reversed and shifted. As such, it is a particular kind of integral transform:
While the symbol t is used above, it need not represent the time domain. But in that context, the convolution formula can be described as a weighted average of the function ƒ(τ) at the moment t where the weighting is given by g(−τ) simply shifted by amount t. As t changes, the weighting function emphasizes different parts of the input function.
More generally, if f and g are complex-valued functions on Rd, then their convolution may be defined as the integral:
Một số tính chất của convolution
- Associativity with scalar multiplication
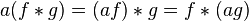
 .
.No algebra of functions possesses an identity for the convolution. The lack of identity is typically not a major inconvenience, since most collections of functions on which the convolution is performed can be convolved with a delta distribution or, at the very least (as is the case of L1) admit approximations to the identity[disambiguation needed]. The linear space of compactly supported distributions does, however, admit an identity under the convolution. Specifically,
- Inverse element
- Complex conjugation
Integration
If ƒ and g are integrable functions, then the integral of their convolution on the whole space is simply obtained as the product of their integrals:Differentiation
In the one-variable case,These identities hold under the precise condition that ƒ and g are absolutely integrable and at least one of them has an absolutely integrable (L1) weak derivative, as a consequence of Young's inequality. For instance, when ƒ is continuously differentiable with compact support, and g is an arbitrary locally integrable function,
In the discrete case, the difference operator D ƒ(n) = ƒ(n + 1) − ƒ(n) satisfies an analogous relationship:
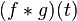
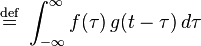
 (
(
![(f * g)[n]\ \stackrel{\mathrm{def}}{=}\
\sum_{m=-\infty}^{\infty} f[m]\, g[n - m]](http://upload.wikimedia.org/math/5/d/2/5d2777af939cdafb39a2988f1c2eae9a.png)
![= \sum_{m=-\infty}^{\infty} f[n-m]\, g[m].](http://upload.wikimedia.org/math/4/3/2/432b9d6de30ebd84ce49f993f8a3a04c.png) (
(
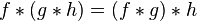









Không có nhận xét nào:
Đăng nhận xét